Zadanie
Marcel sa pri učení na maturitu veľmi nudil. Keďže ho už ani fotenie nenapĺňalo ako predtým, našiel si nové hobby. Naučil sa čarovať. Po istom čase si chcel vyskúšať svoje prvé kúzlo. Dokáže zhmotniť hocijaký predmet z obrazovky počítača. Urobil svoje čáry-máry a kurzor mu v okamihu vyskočil do rúk.
Výtvor v Marcelovi vyvolal údiv. S nadšením si obzeral kurzor zo všetkých strán. Najviac ho však zaujímalo, kde by mohol mať takýto útvar ťažisko? Ako tak dumal nad touto otázkou, vypadol mu kurzor z ruky. Kurzor pád neprežil v celku a odlomil sa mu hrot. Pri smútení nad ulomeným hrotom sa zamyslel nad veľmi zaujímavou kuriozitou. Mohlo sa ťažisko posunúť mimo pôvodne trojuholníkovej časti kurzora?
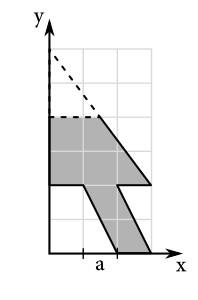
Zamyslite sa a nájdite, kde bolo pôvodné ťažisko kurzora a zistite, či nové ťažisko zostalo vo vnútri trojuholníkovej časti kurzora, alebo sa posunulo von.
Ak chceme nájsť ťažisko nejakého komplikovanejšieho útvaru, tak si ho rozdelíme na nejaké jednoduchšie (napr. trojuholník, rovnobežník, …), pri ktorých vieme určiť ťažisko a ťažisko nášho útvaru je váženým priemerom ťažísk jednoduchších útvarov. Platí pritom, že ako váhu ťažiska určíme hmotnosť tohto jednoduchšieho útvaru. Keďže však kurzor je vyrobený z materiálu s rovnomerne rozloženou hustotou a výška kurzora je všade rovnaká, môžeme hmotnosť zameniť za obsah. Inými slovami, pre každý z jednoduchších útvarov súradnice jeho ťažiska vynásobíme jeho obsahom, tieto súčiny sčítame a výsledok vydelíme obsahom výsledného útvaru. Túto myšlienku si treba zapamätať, pretože sa pri úlohách s ťažiskom častokrát využíva a aj my ju ešte viackrát využijeme pri riešení.
Ťažisko pôvodného kurzora
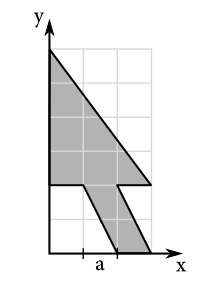
Všimnime si, že kurzor sa pred kolíziou skladal z trojuholníka a rovnobežníka. Ťažisko trojuholníka sa nachádza v tretine výšky trojuholníka, takže súradnice ťažiska trojuholníka sú \(T_{\triangle}=\left[a,\frac{10}3a\right]\). Jeho obsah je \(S_{\triangle}=\frac{3a\cdot4a}{2}=6a^2\). Ťažisko rovnobežníka sa nachádza v priesečníku uhlopriečok, preto sú súradnice ťažiska rovnobežníka \(T_{\lozenge}=\left[2a,a\right]\). Jeho obsah vypočítame ako \(S_{\lozenge}=a\cdot2a=2a^2\). Z týchto informácii vieme súradnice ťažiska kurzora \(T_{\mathrm{kurzor}}\) vypočítať ako: \[ \begin{aligned} x(T_{\mathrm{kurzor}})&=\frac{x(T_{\triangle})S_{\triangle}+x(T_{\lozenge})S_{\lozenge}}{S_{\triangle}+S_{\lozenge}}= \frac{a\cdot6a^2+2a\cdot2a^2}{6a^2+2a^2}=\frac{10a^3}{8a^2}=\frac54a\text,\\ y(T_{\mathrm{kurzor}})&=\frac{y(T_{\triangle})S_{\triangle}+y(T_{\lozenge})S_{\lozenge}}{S_{\triangle}+S_{\lozenge}}= \frac{\frac{10}3a\cdot6a^2+a\cdot2a^2}{6a^2+2a^2}=\frac{22a^3}{8a^2}=\frac{11}4a\text. \end{aligned} \] Ťažisko kurzora pred kolíziou je preto v bode \(T_{\mathrm{kurzor}}=\left[\frac54a,\frac{11}4a\right]\).
Ťažisko kurzora po kolízii
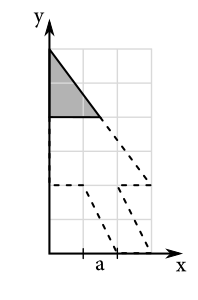
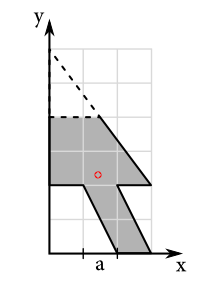
Diskusia
Tu môžte voľne diskutovať o riešení, deliť sa o svoje kusy kódu a podobne.
Pre pridávanie komentárov sa musíš prihlásiť.